コードの成り立ち 〜意味から考える〜

コードを覚えている人は多いでしょう。

ピアノだったらドミソーとかソシレーとか、音楽教室の幼児科で習ったりしますね。
ギターだったらダイアグラムでコードのフォームを丸暗記という感じでしょうか。

でも、そのコードがどういう成り立ち（構成音）なのかをしっかり理解していますか？

成り立ちを覚えてしまえば、コードフォームの丸暗記は必要なくなります。

今回はコードの成り立ちを全5回にわたって解説していきます。

度数がわかっているという前提でないと話が進んでいかないので
度数ってなに？って人はこちらの記事を参考に。
（度数について　〜音の距離感〜）

コードとは

コードというのは、高さ（音程）が異なる複数の音を同時に鳴らすことです。
日本語では和音といいますね。

ここでいう高さが異なるというのは、ピッチクラス（同じ音名を与えられたもの）が異なるという意味です。

低いドと高いドは同じ「ド」という音名が与えられているため、複数とはみなしません。
音名が異なると考えればわかりやすいでしょう。

そして複数といいましたが、2つではダメです。
最低でも3音必要になります。

一つの楽器でコードとして成立させる場合は、一人で3音出す必要があります。
バンドで、ベース・ギター・ピアノなどがそれぞれ一つずつしか音を出していなくても音名の違う音を出していれば、バンド全体としてはコードが成立します。

なぜ3音かというと、コードの大まかな方向性を決定づけるのに必要な音数が3音だからです。
これだけ聞くとチンプンカンプンでしょう（笑）

コードには方向性があります。
人によって感じ方は違うでしょうから、あくまで一般論になりますが「明るい・暗い」や「安定・不安定」という方向性です。

これらを決定づけるために3音必要になってくるわけです。

そして3音以上の音を、どれでもテキトーに鳴らせばいいわけではありません。

決まったルール（度数）で音を重ねていく必要があります。

まずは定番どころをおさえていきましょう。

「明るい・暗い」のメジャーコードとマイナーコードです。
メジャーコードは明るい響きに、マイナーコードは暗い響きに感じます。

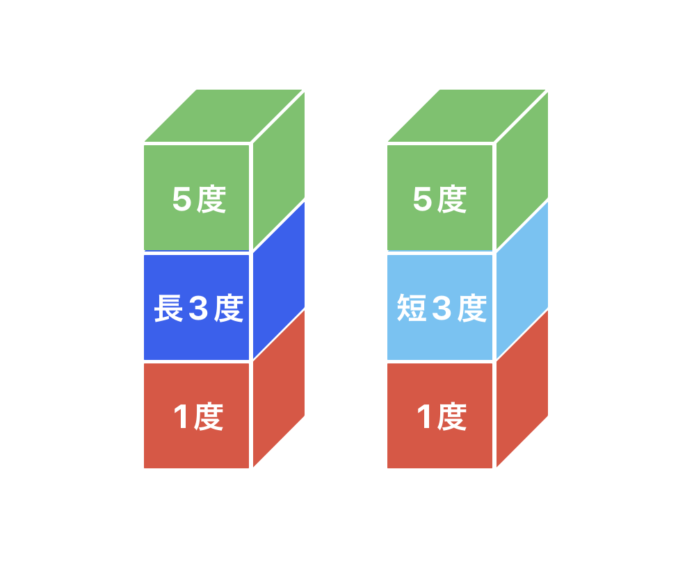
メジャーコードの構成音は1度（ルート）・長3度・5度となります。

この1・3・5度の音を重ねるというのが、メジャーコードのルールです。
C（ド）のメジャーコードならば「CEG(ドミソ)」です。

1・3・5番目の音か〜、と思ったそこのアナタ
ゲンコツです（笑）

コードの考え方で重要なのは度数、つまり基準となる音からの距離感です。
単純に1・3・5と考えてはいけません。

D（レ）のメジャーコードは「DFA（レファラ）」ではなく「DF#A（レファ#ラ）」なのです。
長3度というのは基準の音（ルート）から全音・全音離れたところを意味します。
E（ミ）とF（ファ）が半音しか離れていないため、Dからみた全音・全音はF#となるわけです。

何度も言いますが、度数がわかっている前提で進めているので
度数や全音・半音の意味がわからない人は前述の記事を読んでください。

マイナーコードの構成音は1度（ルート）・短3度・5度となります。
C（ド）のマイナーコードならば「CE♭G(ドミ♭ソ)」です。

D（レ）のマイナーコードは「DFA（レファラ）」となりますね。

CメジャーはCEG、CマイナーはCE♭Gつまりメジャーとマイナーの違いは、3度の部分たった一音です。ここが長3度なのか短3度なのかで、コード全体の響きがガラッと変わります。

基準の音があり、3度の長短で明るいか暗いかを決定づけるというわけですね。
うんうん、なるほどじゃ5度は何してんの？（笑）

5度はね、「安定・不安定」の部分を担っています。
通常の5度は「安定」です。ということは「不安定」な5度もあるというわけです。
これはまた別の回に。

メジャーコードは、明るく（長3度）安定な（5度）コード
マイナーコードは、暗く（短3度）安定な（5度）コード
という方向性を持ちます。

安定・不安定といってもコードが完全・不完全とか、成立する・しないといったことではなく
安心感があるかないか、といったニュアンスです。
落ち着く・落ち着かない、でもいいですね。

まずはこの2種類をしっかり押さえると良いでしょう。
ピアノをイメージするとわかりやすいですが、白鍵・黒鍵は規則正しく並んでいるわけではありません。

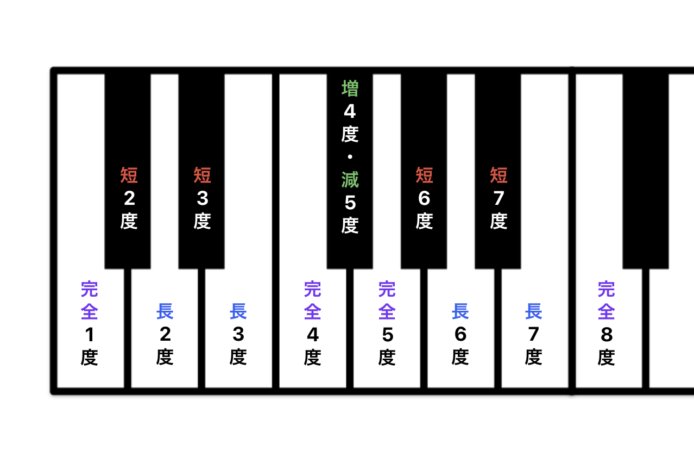
白黒白黒白白黒白黒白黒白白となっています。
白黒白墨白白黒白黒百黒白自って書いてもバレんかな（笑）

C（ド）から見たD（レ）と、E（ミ）から見たF（ファ）は距離感が違います。
ここが非常に厄介なところです。
コードや度数を勉強しようと思った人が、必ずと言っていいほどひっかかるところです。

非常に重要なところなので何度も反復して覚えていきましょう★
「コードの成り立ち　その２」に続きます。